Mientras aún estaba en la escuela, su familia planeó que siguiera la carrera de arquitectura de su padre, pero las malas calificaciones y la aptitud para el dibujo y el diseño finalmente lo llevaron a una carrera en las artes gráficas. Su obra pasó casi desapercibida hasta la década de 1950, pero en 1956 había realizado su primera exposición importante, fue publicada en la revista Time y adquirió fama mundial. Entre sus mayores admiradores se encontraban los matemáticos, quienes reconocieron en su obra una extraordinaria visualización de los principios matemáticos. Esto fue más notable en el sentido de que Escher no tenía una formación matemática formal más allá de la escuela secundaria.
Teselaciones
Las divisiones regulares del plano, llamadas "teselaciones", son arreglos de formas cerradas que cubren completamente el plano sin superponerse y sin dejar huecos. Normalmente, las formas que componen una teselación son polígonos o formas regulares similares, como las baldosas cuadradas que se utilizan a menudo en los suelos. Sin embargo, Escher estaba fascinado por todo tipo de teselados, regulares e irregulares, y se deleitaba especialmente con lo que llamó "metamorfosis", en las que las formas cambiaban e interactuaban entre sí y, a veces, incluso se liberaban del plano.
 |
| Boceto de la Alhambra |
Su interés comenzó en 1936, cuando viajó a España y vio los patrones de azulejos utilizados en la Alhambra. Pasó muchos días esbozando estos detalles y luego afirmó que esta "era la fuente de inspiración más rica que jamás haya aprovechado". En 1957 escribió un ensayo sobre teselados, en el que comentó:
En los sectores matemáticos, la división regular del plano se ha considerado teóricamente. . . ¿Significa esto que se trata de una cuestión exclusivamente matemática? En mi opinión, no es así. [Los matemáticos] han abierto la puerta que conduce a un dominio extenso, pero ellos mismos no han entrado en este dominio. Por su propia naturaleza, están más interesados en la forma en que se abre la puerta que en el jardín que está detrás de ella.
Sea o no justo para los matemáticos, es cierto que habían demostrado que de todos los polígonos regulares, solo el triángulo, el cuadrado y el hexágono pueden usarse para una teselación. (Muchos más polígonos irregulares forman mosaicos en el plano; en particular, hay muchos teselados que utilizan pentágonos irregulares). Escher aprovechó estos patrones básicos en sus teselados, aplicando lo que los geómetras llamarían reflejos, reflejos de deslizamiento, traslaciones y rotaciones para obtener una mayor variedad de patrones. . También elaboró estos patrones "distorsionando" las formas básicas para convertirlas en animales, pájaros y otras figuras. Estas distorsiones tenían que obedecer a la simetría de tres, cuatro o seis veces del patrón subyacente para preservar la teselación. El efecto puede ser sorprendente y hermoso.
Poliedros
Los sólidos regulares, conocidos como poliedros, cautivaron especialmente a Escher. Los convirtió en el tema de muchas de sus obras y los incluyó como elementos secundarios en muchas más. Solo hay cinco poliedros con caras poligonales exactamente similares, y se denominan sólidos platónicos: el tetraedro, con cuatro caras triangulares; el cubo, de seis caras cuadradas; el octaedro, con ocho caras triangulares; el dodecaedro, con doce caras pentagonales; y el icosaedro, con veinte caras triangulares. En el grabado en madera Cuatro sólidos regulares, Escher ha cruzado todos los sólidos platónicos menos uno de tal manera que sus simetrías están alineadas, y los ha hecho translúcidos para que cada uno sea discernible a través de los demás. Cual falta?
Hay muchos sólidos interesantes que pueden obtenerse de los sólidos platónicos intersecándolos o estelándolos. Estrellar un sólido significa reemplazar cada una de sus caras por una pirámide, es decir, por un sólido puntiagudo de caras triangulares; esto transforma el poliedro en una estrella puntiaguda y tridimensional. Un hermoso ejemplo de un dodecaedro estrellado se puede encontrar en El orden y el caos de Escher. Aquí la figura estrellada descansa dentro de una esfera cristalina, y la austera belleza de la construcción contrasta con los restos desordenados de otros elementos que descansan sobre la mesa. Observe que se puede adivinar la fuente de luz para la composición, ya que la ventana brillante arriba y a la izquierda del espectador se refleja en la esfera.
Los sólidos que se cruzan también están representados en muchas de las obras de Escher, siendo una de las más interesantes las estrellas grabadas en madera.
Aquí hay sólidos construidos con octaedros, tetraedros y cubos que se cruzan, entre muchos otros. Uno podría hacer una pausa para considerar que si Escher simplemente hubiera dibujado un montón de formas matemáticas y lo hubiera dejado así, probablemente nunca hubiéramos oído hablar de él o de su trabajo. En cambio, mediante dispositivos como colocar a los camaleones dentro del poliedro para burlarse de nosotros y alarmarnos, Escher nos saca de nuestros cómodos hábitos de percepción y nos desafía a mirar con ojos nuevos las cosas que ha forjado. Sin duda, esta es otra fuente de la admiración de los matemáticos por el trabajo de Escher, ya que esa frescura perceptiva se encuentra detrás de todo gran descubrimiento matemático.
La forma del espacio
Entre las obras más importantes de Escher desde un punto de vista matemático se encuentran las que tratan de la naturaleza del espacio mismo. Su grabado en madera Three Intersecting Planes es un buen lugar para comenzar una revisión de estas obras, ya que ejemplifica la preocupación del artista por la dimensionalidad del espacio y por la capacidad de la mente para discernir la tridimensionalidad en una representación bidimensional. Como veremos en la siguiente sección, Escher a menudo explotó esta última característica para lograr efectos visuales asombrosos.
Inspirado en un dibujo de un libro del matemático H.S.M Coxeter, Escher creó muchas representaciones hermosas del espacio hiperbólico, como en el grabado en madera Circle Limit III. Este es uno de los dos tipos de espacio no euclidiano, y el modelo representado en la obra de Escher se debe en realidad al matemático francés Poincaré. Para tener una idea de cómo es este espacio, imagina que estás realmente en la imagen. A medida que camina desde el centro de la imagen hacia su borde, se encogerá como lo hacen los peces en la imagen, de modo que para llegar realmente al borde tendrá que caminar una distancia que, para usted, le parecerá infinita. De hecho, para usted, al estar dentro de este espacio hiperbólico, no sería inmediatamente obvio que algo fuera inusual en él; después de todo, también debe caminar una distancia infinita para llegar al borde del espacio euclidiano ordinario. Sin embargo, si fueras un observador cuidadoso, podrías comenzar a notar algunas cosas extrañas, como que todos los triángulos similares eran del mismo tamaño y que ninguna figura de lados rectos que pudieras dibujar tendría cuatro ángulos rectos, es decir, este espacio no no tiene cuadrados ni rectángulos. ¡Un lugar realmente extraño!
Aún más inusual es el espacio sugerido por el grabado en madera de Serpientes. Aquí el espacio se dirige hacia el infinito tanto hacia el borde como hacia el centro del círculo, como lo sugieren los anillos entrelazados que se encogen. Si ocuparas este tipo de espacio, ¿cómo sería?
Además de las geometrías euclidianas y no euclidianas, Escher estaba muy interesado en los aspectos visuales de la topología, una rama de las matemáticas que acababa de florecer durante su vida. La topología se ocupa de aquellas propiedades de un espacio que no se modifican por distorsiones que pueden estirarlo o doblarlo, pero que no lo desgarran ni perforan, y los topólogos estaban ocupados mostrando al mundo muchos objetos extraños. La tira de Möbius es quizás el mejor ejemplo, y Escher hizo muchas representaciones de ella. Tiene la curiosa propiedad de que tiene un solo lado y un borde. Por lo tanto, si rastrea el camino de las hormigas en Möbius Strip II, descubrirá que no caminan en lados opuestos de la franja, sino que todas caminan por el mismo lado. Es fácil hacer una tira de Möbius; simplemente corte una tira de papel con unas tijeras, gírela hasta la mitad y luego pegue o pegue los extremos con cinta adhesiva. ¿Qué predice que sucederá si intenta cortar una tira de este tipo en dos, a lo largo?
Otra litografía muy notable, llamada Print Gallery, explora tanto la lógica como la topología del espacio. Aquí un joven en una galería de arte está mirando una impresión de una ciudad costera con una tienda a lo largo de los muelles, y en la tienda hay una galería de arte, con un joven mirando una impresión de una ciudad costera ... pero espere ! ¿Qué ha pasado?
Todas las obras de Escher recompensan una mirada prolongada, pero esta lo hace especialmente. De alguna manera, Escher ha convertido el espacio en sí mismo, de modo que el joven está tanto dentro como fuera de la imagen simultáneamente. El secreto de su elaboración puede hacerse algo menos oscuro examinando el boceto en papel cuadriculado que el artista hizo al preparar esta litografía. Observe cómo la escala de la cuadrícula crece continuamente en el sentido de las agujas del reloj. Y fíjate especialmente en lo que implica este truco: un agujero en el medio. Un matemático llamaría a esto una singularidad, un lugar donde la estructura del espacio ya no se mantiene unida. Simplemente no hay forma de unir este extraño espacio en un todo sin costuras, y Escher, en lugar de tratar de ocultarlo de alguna manera, ha puesto sus iniciales de marca registrada justo en el centro.
La lógica del espacio
Por "lógica" del espacio nos referimos a las relaciones espaciales entre objetos físicos que son necesarias y que, cuando se violan, dan como resultado paradojas visuales, a veces llamadas ilusiones ópticas. Todos los artistas están preocupados por la lógica del espacio y muchos han explorado sus reglas con bastante deliberación. Picasso, por ejemplo.
Escher comprendió que la geometría del espacio determina su lógica y, de la misma forma, la lógica del espacio a menudo determina su geometría. Una de las características de la lógica del espacio que a menudo aplicó es el juego de luces y sombras en objetos cóncavos y convexos. En la litografía Cubo con cintas, las protuberancias en las bandas son nuestra pista visual de cómo se entrelazan con el cubo. Sin embargo, si vamos a creer lo que ven nuestros ojos, ¡no podemos creer las cintas!
Otra de las principales preocupaciones de Escher era la perspectiva. En cualquier dibujo en perspectiva, se eligen puntos de fuga que representan para el ojo el (los) punto (s) en el infinito. Fue el estudio de la perspectiva y los "puntos en el infinito" de Alberti, Desargues y otros durante el renacimiento lo que condujo directamente al campo moderno de la geometría proyectiva.
Al introducir puntos de fuga inusuales y obligar a los elementos de una composición a obedecerlos, Escher pudo renderizar escenas en las que las orientaciones "arriba / abajo" e "izquierda / derecha" de sus elementos cambian, dependiendo de cómo el ojo del espectador lo perciba. En su estudio de perspectiva para High and Low, el artista ha colocado cinco puntos de fuga: arriba a la izquierda y derecha, abajo a la izquierda y derecha y al centro. El resultado es que en la mitad inferior de la composición el espectador mira hacia arriba, pero en la mitad superior mira hacia abajo. Para enfatizar lo que ha logrado, Escher ha realizado las representaciones de las mitades superior e inferior de la misma composición.
Un tercer tipo de "dibujo imposible" se basa en la insistencia del cerebro en utilizar pistas visuales para construir un objeto tridimensional a partir de una representación bidimensional, y Escher creó muchos trabajos que abordan este tipo de anomalía.
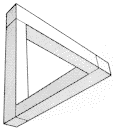
Uno de los más intrigantes se basa en una idea del matemático Roger Penrose: el triángulo imposible. En esta litografía, Cascada, dos triángulos de Penrose se han combinado en una figura imposible. Uno ve de inmediato una de las razones por las que la lógica del espacio debe excluir tal construcción: la cascada es un sistema cerrado, pero gira la rueda del molino continuamente, como una máquina de movimiento perpetuo, violando la ley de conservación de la energía. (Observe los cubos y octaedros que se cruzan en las torres).
Autorreferencia e información
Nuestra consideración final del arte de Escher involucra su relación con los campos de la ciencia de la información y la inteligencia artificial. Este aspecto de su trabajo se ha pasado por alto en gran medida en estudios anteriores, pero Douglas R. Hofstadter en su libro ganador del Premio Pulitzer de 1980, Gödel, Escher, Bach: An Eternal Golden Braid, defendió su importancia en estos campos.
Un concepto central que capturó Escher es el de la autorreferencia, que muchos creen que se encuentra cerca del corazón del enigma de la conciencia, y la capacidad del cerebro para procesar información de una manera que ninguna computadora ha imitado con éxito hasta ahora.
La litografía Drawing Hands y el grabado en madera Fish and Scales capturan esta idea de una manera diferente. En el primero, la autorreferencia es directa y conceptual; las manos se dibujan en gran medida de la manera en que la conciencia se considera y se construye a sí misma, misteriosamente, siendo el yo y la autorreferencia inseparables y iguales. En Fish and Scales, por otro lado, la autorreferencia es más funcional; uno podría más bien llamarlo auto-semejanza. De esta manera, el grabado en madera describe no solo a los peces sino a todos los organismos, porque aunque no estamos construidos, al menos físicamente, a partir de pequeñas copias de nosotros mismos, en un sentido teórico de la información, de hecho estamos construidos de esa manera, para cada célula de nuestros cuerpos llevan la información completa que describe a toda la criatura, en forma de ADN.
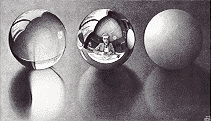
En un nivel más profundo, la autorreferencia se encuentra en la forma en que nuestros mundos de percepción se reflejan y se cruzan entre sí. Cada uno de nosotros es como un personaje de un libro que está leyendo su propia historia, o como la imagen de un espejo que refleja su propio paisaje. Muchas de las obras de Escher exhiben este tema de mundos que se cruzan, pero aquí consideraremos solo uno de los ejemplos. Como es común en el tratamiento de Escher de esta idea, la litografía Three Spheres II hace uso de las propiedades reflectantes de un espejo esférico. Aquí, como señaló Hofstatder, "cada parte del mundo parece contener y estar contenida en todas las demás partes ..." Las esferas se relacionan entre sí, el artista, la habitación en la que trabaja y el papel sobre el que dibuja las esferas.
Y así terminamos donde comenzamos, con un autorretrato: la obra es un reflejo del artista, el artista reflejado en su obra.
Conclusión
Aquí hemos considerado sólo un puñado entre los cientos de dibujos, litografías, xilografías y entrepisos que Escher nos dejó a su muerte en 1972. Mucho más podría decirse, y se ha dicho, sobre la profundidad, el significado y la importancia de su obra. trabaja. Se anima al lector a explorar más a fondo el rico legado de M.C. Escher, y reflexionar nuevamente sobre las intersecciones que nos ha trazado entre el mundo de la imaginación, el mundo de las matemáticas y el mundo de nuestra vida de vigilia.














No hay comentarios:
Publicar un comentario