En geometría, describimos un punto P que divide un segmento AB en dos partes, tal que su razón es 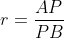
Ahora veamos cómo calcular las coordenadas de un punto P(x,y) que divide a un segmento AB en un sistema cartesiano
Observemos la siguiente figura:
Al trasponer términos, obtenemos la razón:
Ahora veamos cómo calcular las coordenadas de un punto P(x,y) que divide a un segmento AB en un sistema cartesiano
Observemos la siguiente figura:
Al trasponer términos, obtenemos la razón:
De esta última expresión, despejamos x:
De manera análoga, podemos obtener la coordenada si trazamos perpendiculares al eje Y, esto es
Notas:
En geometría analítica se debe considerar el signo de r, ya que tratamos con segmentos dirigidos.
Si el punto de división P es externo al segmento dirigido AB, entonces r es negativa (AP y PB tienen sentidos contrarios)
Ejemplo:
Obtener las coordenadas del punto que divide al segmento con extremos A(3,-1) y B(-5,5) en la razón r=3/5.
Solución:
x1= 3
x2=-5
y1= -1
y2=5
El punto de división se encuentra en P(0,5/4), como se puede verse en la figura:
Vamos a definir el segmento como se vio en esta entrada
Definimos un Segmento definiendo los puntos con los comandos A =(3,-1) y B =(-5,5) más el comando Segmento[A,B]. Del mismo modo, definimos r=3/5
Posteriormente procedemos a calcular cada coordenada del punto de división con el siguiente comando:
P=((x(A)+r*x(B))/(1+r), (y(A)+r*y(B))/(1+r))
y de esta forma se crea el punto de división P:





Es un tema de gran interés en la forma de como explican con imágenes y ejemplos es mas entendible
ResponderEliminarMuy buena información, lo(s) felicito por esta maravillosa explicación que han echo.
ResponderEliminarSigan así suerte