Círculo

Se puede usar la fórmula de la distancia que presentamos en una entrada anterior para definir un conjunto de puntos en el plano coordenado. Uno de esos muy importantes conjuntos se define como sigue.

Definición 1: Círculo 

Un círculo es el conjunto de todos los puntos P(x, y) en el plano coordenado que están a determinada distancia fija r, llamada radio, de un punto fijo dado C, llamado centro.  

Si las coordenadas del centro son C(h, k) entonces, de acuerdo con la definición anterior,  un punto P (x, y) está en un círculo de radio r si y sólo si 

Ya que  (x – h) ² + (y – k)² =r² siempre es no negativo, se obtiene una ecuación equivalente si los  dos lados se elevan al cuadrado. Llegamos a la conclusión de que un círculo de radio r y  centro C(h, k) tiene la ecuación

(Ec. 1) 

FIGURA A

FIGURA B

En la FIGURA A hemos trazado una gráfica típica de una ecuación con la forma de la ecuación (Ec1). La ecuación (Ec.1) se llama forma normal, estándar o canónica de la ecuación de un  círculo. Se ve que los símbolos h y k en (Ec.1) representan números reales, y como tales pueden  ser positivos, cero o negativos. Cuando h = 0 y k = 0, se ve que la forma normal de la ecuación de un círculo con centro en el origen es (FIGURA B)

  (Ec.2)

Cuando r = 1 se dice que (Ec. 1) o (Ec. 2) es una ecuación de un círculo unitario. Por ejemplo, x²+y²=1 es una ecuación de un círculo unitario con centro en el origen.

Ejemplo 1: Centro y Radio:

Determine el centro y el radio del círculo cuya ecuación es:

Solución: Para obtener la forma normal de la ecuación (4) se escribe como sigue:

Al comparar esta última forma se identifican h = -5, k = 2  r =√2. Así, el círculo tiene su centro en C(8, -2) y su radio es 7

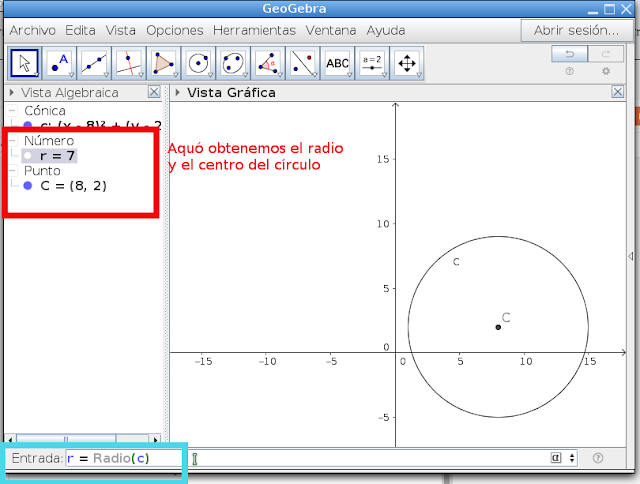
En Geogebra:

Escribimos la ecuación directamente en la barra de entrada para crear el círculo

Con esto geogebra realiza la gráfica de la ecuación y le da un nombre a la circunferencencia, en este caso (c)

 

Centro y radio:

Con los comandos:

C= Centro(c)
r = Radio(c)

Calculos los valores de centro y radio del cículo.

Ejemplo 2: Ecuación de un Círculo

Halle la ecuación del círculo cuyo centro es C=(-5, 4)  y cuyo radio es √2 .
 

Solución:
Al sustituir h=5, k = 4 y r = √2 en la ecuación (Ec. 1) se obtiene:

 

En Geogebra:

Usamos el Comando Circunferencia(centro, radio) para crear la ecuación del círculo.

Circunferencia[(-5, 4), sqrt(2)]